Building a CHIP-8 Emulator [C++]
I’ve always loved emulators because they let me play old games that I enjoyed as a kid, so I thought it might be fun to learn how they work and how to build one. My real goal is to build an NES emulator, but after doing some research, I decided to take the advice of the internet and start by building an emulator for the much less complex CHIP-8 instead. It’s a good stepping stone to the NES.
There are a lot of CHIP-8 emulators out there, and a lot of websites about building them, but I noticed a divide between the two. There might be code without a lot of explanation, or explanations without a lot of code. Those are fine for an experienced programmer who can fill in the gaps, but I want to provide a holistic reference for the inexperienced. Not only do I hope to show how to build a simple emulator, but I also hope to teach some low-level computer fundamentals.
The only requirement is a basic understanding of C++.
How Does a CPU Work?
Before we can talk about emulators, we first need a basic understanding of how a CPU works.
A CPU reads instructions from somewhere in memory that tell it what to do. A CPU may be really fast but it’s stupid. You have to be very explicit and logical to get it to do what you want and you do that using a discrete set of instructions.
For example, consider this instruction for the CPU inside of the original Game Boy: $C622. It encodes an operation and relevant data into a number that a machine can read.
Different instructions are encoded in different ways. In this case, the first byte ($C6) says ADD to Register A, and the second byte ($22) is the value that will be added to Register A. So this instruction says Add $22 to Register A.
As explained above, the CHIP-8 was not a real physical CPU but instead a virtual machine with its own instruction set, but the same principles apply. For example, consider the CHIP-8 instruction $7522. The first byte ($75) says ADD to Register 5 and the second byte ($22) is the value to be added to Register 5. So this instruction says ADD $22 to Register 5.
See the Appendix for more info.
Way back in the day, programmers would write programs in an assembly language rather than the high-level languages (like C++) that we use today. Assembly is as low as you can go while still being human readable. An assembler would translate their human-readable assembly into the 1s and 0s that the computer could understand.
Keeping with the earlier example, the assembly program would have ADD V5, $22, and the assembler would translate that to $7522, which the CHIP-8 interpreter can read. The same thing happens today, only we have another layer above assembly in the form of high-level languages.
What is an Emulator?
An emulator reads the original machine code instructions that were assembled for the target machine, interprets them, and then replicates the functionality of the target machine on the host machine. The ROM files contain the instructions, the emulator reads those instructions, and then does work to mimic the original machine.
When an emulator reads the instruction $7522, it would emulate the behavior of the CHIP-8 by doing something like this:
| |
That’s really all there is to it. When emulating more advanced machines you also have to emulate other components like the graphics processor and the sound chip. The CHIP-8 is a nice starting project because the CPU only has 34 instructions, the graphics are simple monochrome pixels, and the sounds are just a single buzzer tone.
CHIP-8 Description
We’d like to mimic the components of a CHIP-8 in our emulator, so let’s describe them.
16 8-bit Registers
A register is a dedicated location on a CPU for storage. Any operations that a CPU does must be done within its registers. A CPU typically only has a few registers, so long-term data is held in memory instead. Operations often involve loading data from memory into registers, operating on those registers, and then storing the result back into memory.
The CHIP-8 has sixteen 8-bit registers, labeled V0 to VF. Each register is able to hold any value from 0x00 to 0xFF.
Register VF is a bit special. It’s used as a flag to hold information about the result of operations.
4K Bytes of Memory
There is relatively little register-space (because it’s expensive), so a computer needs a large chunk of general memory dedicated to holding program instructions, long-term data, and short-term data. It references different locations in that memory using an address.
The CHIP-8 has 4096 bytes of memory, meaning the address space is from 0x000 to 0xFFF.
The address space is segmented into three sections:
0x000-0x1FF: Originally reserved for the CHIP-8 interpreter, but in our modern emulator we will just never write to or read from that area. Except for…
0x050-0x0A0: Storage space for the 16 built-in characters (0 through F), which we will need to manually put into our memory because ROMs will be looking for those characters.
0x200-0xFFF: Instructions from the ROM will be stored starting at 0x200, and anything left after the ROM’s space is free to use.
16-bit Index Register
The Index Register is a special register used to store memory addresses for use in operations. It’s a 16-bit register because the maximum memory address (0xFFF) is too big for an 8-bit register.
16-bit Program Counter
As mentioned earlier, the actual program instructions are stored in memory starting at address 0x200. The CPU needs a way of keeping track of which instruction to execute next.
The Program Counter (PC) is a special register that holds the address of the next instruction to execute. Again, it’s 16 bits because it has to be able to hold the maximum memory address (0xFFF).
An instruction is two bytes but memory is addressed as a single byte, so when we fetch an instruction from memory we need to fetch a byte from PC and a byte from PC+1 and connect them into a single value. We then increment the PC by 2 because We have to increment the PC before we execute any instructions because some instructions will manipulate the PC to control program flow. Some will add to the PC, some will subtract from it, and some will change it completely.
16-level Stack
A stack is a way for a CPU to keep track of the order of execution when it calls into functions. There is an instruction (CALL) that will cause the CPU to begin executing instructions in a different region of the program. When the program reaches another instruction (RET), it must be able to go back to where it was when it hit the CALL instruction. The stack holds the PC value when the CALL instruction was executed, and the RETURN statement pulls that address from the stack and puts it back into the PC so the CPU will execute it on the next cycle.
The CHIP-8 has 16 levels of stack, meaning it can hold 16 different PCs. Multiple levels allow for one function to call another function and so on, until they all return to the original caller site.
Putting a PC onto the stack is called pushing and pulling a PC off of the stack is called popping.
8-bit Stack Pointer
Similar to how the PC is used to keep track of where in memory the CPU is executing, we need a Stack Pointer (SP) to tell us where in the 16-levels of stack our most recent value was placed (i.e, the top).
We only need 8 bits for our stack pointer because the stack will be represented as an array, so our stack pointer can just be an index into that array. We only need sixteen indices then, which a single byte can manage.
When we pop a value off the stack, we won’t actually delete it from the array but instead just copy the value and decrement the SP so it “points” to the previous value.
Let’s go through an example of how the stack works. Here is the example program we’re running, with the address of the instruction on the left and the actual instruction on the right. Don’t worry about the LD instructions, just focus on the __CALL__s and the __RET__s. A JMP is like a CALL, but it doesn’t put anything onto the stack.
| |
Initially the stack pointer starts at 0, indicating the top of the stack, and the stack itself is just an array filled with zeroes. As we execute CALLs and RETs, we’ll see what the stack does.
| |
With each CALL, the current PC (which was previously incremented to point to the next instruction) is placed where the SP was pointing, and the SP is incremented.
With each RET, the stack pointer is decremented by one and the address that it’s pointing to is put into the PC for execution.
The actual order of execution looks like this:
| |
8-bit Delay Timer
The CHIP-8 has a simple timer used for timing. If the timer value is zero, it stays zero. If it is loaded with a value, it will decrement at a rate of 60Hz.
Rather than making sure that the delay timer actually decrements at a rate of 60Hz, I just decrement it at whatever rate we have the cycle clock set to (discussed later) which has worked fine for all the games I’ve tested.
8-bit Sound Timer
The CHIP-8 also has another simple timer used for sound. Its behavior is the same (decrementing at 60Hz if non-zero), but a single tone will buzz when it’s non-zero. Programmers used this for simple sound emission.
While I do have a sound timer in my implementation, I opted to not bother with making the application actually emit any sound. See here for a way to generate a tone with SDL.
16 Input Keys
The CHIP-8 has 16 input keys that match the first 16 hex values: 0 through F. Each key is either pressed or not pressed.
I used the input mapping recommended here.
| |
64x32 Monochrome Display Memory
The CHIP-8 has an additional memory buffer used for storing the graphics to display. It is 64 pixels wide and 32 pixels high. Each pixel is either on or off, so only two colors can be represented.
Understanding and then emulating its operation is probably the most challenging part of the entire project (but still very easy compared to the NES).
I’ll cover the exact implementation of the draw instruction down below, but first let’s cover how the drawing works. As mentioned, a pixel can be either on or off. In our case, we’ll use a uint32 for each pixel to make it easy to use with SDL (discussed later), so on is 0xFFFFFFFF and off is 0x00000000.
The draw instruction iterates over each pixel in a sprite and XORs the sprite pixel with the display pixel.
- Sprite Pixel Off XOR Display Pixel Off = Display Pixel Off
- Sprite Pixel Off XOR Display Pixel On = Display Pixel On
- Sprite Pixel On XOR Display Pixel Off = Display Pixel On
- Sprite Pixel On XOR Display Pixel On = Display Pixel Off
In other words, a display pixel can be set or unset with a sprite. This is often done to only update a specific part of the screen. If you knew you had drawn a sprite at (X,Y) and you now want to draw it at (X+1,Y+1), you could first issue a draw command again at (X,Y) which would erase the sprite, and then you could issue another draw command at (X+1,Y+1) to draw it in the new location. This is why moving objects in CHIP-8 games flicker.
As an example, let’s pretend we have a blank screen that is 16x10.

We draw a 10x4 sprite at (1,1), so it extends from (1,1) to (10,4).

We then draw an 8x2 sprite at (6,6), so it extends from (6,6) to (13,7).

If we then draw a 3x4 sprite at (7,3), it would cut a piece out of each of them and draw a line in the gap. The overlapping pixels would turn off (on XOR on = off), and the off pixels would turn on (off XOR on = on).
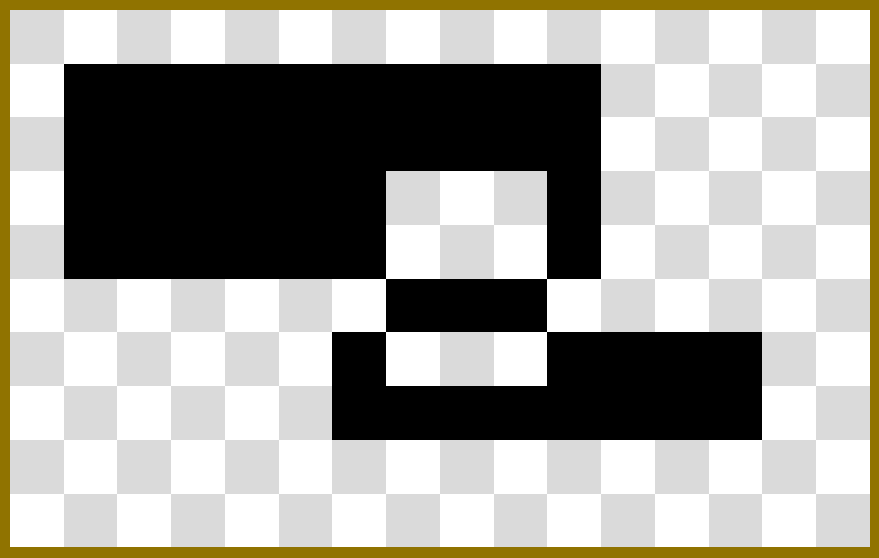
Some references I’ve read say that a sprite should wrap around to the other side of the screen if attempting to draw off-screen, so that’s what we’ll do.
Class Members
Given the aforementioned components, our class data could look like this:
| |
Loading a ROM
Before we can execute instructions, we need to have those instructions in memory, so we’ll need a function that loads the contents of a ROM file.
| |
As mentioned earlier, the Chip8’s memory from 0x000 to 0x1FF is reserved, so the ROM instructions must start at 0x200.
We also want to initially set the PC to 0x200 in the constructor because that will be the first instruction executed.
| |
Loading the Fonts
There are sixteen characters that ROMs expected at a certain location so they can write characters to the screen, so we need to put those characters into memory.
The characters are examples of sprites, which we’ll see more of later. Each character sprite is five bytes.
The character F, for example, is 0xF0, 0x80, 0xF0, 0x80, 0x80. Take a look at the binary representation:
| |
Can you see it? Each bit represents a pixel, where a 1 means the pixel is on and a 0 means the pixel is off.
We need an array of these bytes to load into memory. There are 16 characters at 5 bytes each, so we need an array of 80 bytes.
| |
We can then load them into memory starting at 0x50 in our constructor.
| |
Random Number Generator
There is an instruction which places a random number into a register. With physical hardware this could be achieved by, reading the value from a noisy disconnected pin or using a dedicated RNG chip, but we’ll just use C++’s built in random facilities.
We’ll need to add two member variables and seed the RNG in the constructor. A simple seed is the system clock.
| |
We can then get a random number between 0 and 255 by using randByte.
The Instructions
The CHIP-8 has 34 instructions that we need to emulate.
I’ll show the opcode and its description, add any needed helpful info, and show an implementation in code. The opcode list and descriptions are taken from here.
It's likely that the test ROMs were built referencing the same possibly erroneous reference, which is why they fail when using the actual correct implementation. I'm not going to worry about it, but feel free to use the second reference instead if you like. Just be aware that the test ROMs used at the end will fail for you.
See here for more info.
00E0: CLS
Clear the display.
We can simply set the entire video buffer to zeroes.
| |
00EE: RET
Return from a subroutine.
The top of the stack has the address of one instruction past the one that called the subroutine, so we can put that back into the PC. Note that this overwrites our preemptive pc += 2 earlier.
| |
1nnn: JP addr
Jump to location nnn.
The interpreter sets the program counter to nnn.
A jump doesn’t remember its origin, so no stack interaction required.
| |
2nnn - CALL addr
Call subroutine at nnn.
When we call a subroutine, we want to return eventually, so we put the current PC onto the top of the stack. Remember that we did pc += 2 in Cycle(), so the current PC holds the next instruction after this CALL, which is correct. We don’t want to return to the CALL instruction because it would be an infinite loop of CALLs and RETs.
| |
3xkk - SE Vx, byte
Skip next instruction if Vx = kk.
Since our PC has already been incremented by 2 in Cycle(), we can just increment by 2 again to skip the next instruction.
| |
4xkk - SNE Vx, byte
Skip next instruction if Vx != kk.
Since our PC has already been incremented by 2 in Cycle(), we can just increment by 2 again to skip the next instruction.
| |
5xy0 - SE Vx, Vy
Skip next instruction if Vx = Vy.
Since our PC has already been incremented by 2 in Cycle(), we can just increment by 2 again to skip the next instruction.
| |
6xkk - LD Vx, byte
Set Vx = kk.
| |
7xkk - ADD Vx, byte
Set Vx = Vx + kk.
| |
8xy0 - LD Vx, Vy
Set Vx = Vy.
| |
8xy1 - OR Vx, Vy
Set Vx = Vx OR Vy.
| |
8xy2 - AND Vx, Vy
Set Vx = Vx AND Vy.
| |
8xy3 - XOR Vx, Vy
Set Vx = Vx XOR Vy.
| |
8xy4 - ADD Vx, Vy
Set Vx = Vx + Vy, set VF = carry.
The values of Vx and Vy are added together. If the result is greater than 8 bits (i.e., > 255,) VF is set to 1, otherwise 0. Only the lowest 8 bits of the result are kept, and stored in Vx.
This is an ADD with an overflow flag. If the sum is greater than what can fit into a byte (255), register VF will be set to 1 as a flag.
| |
8xy5 - SUB Vx, Vy
Set Vx = Vx - Vy, set VF = NOT borrow.
If Vx > Vy, then VF is set to 1, otherwise 0. Then Vy is subtracted from Vx, and the results stored in Vx.
| |
8xy6 - SHR Vx
Set Vx = Vx SHR 1.
If the least-significant bit of Vx is 1, then VF is set to 1, otherwise 0. Then Vx is divided by 2.
A right shift is performed (division by 2), and the least significant bit is saved in Register VF.
| |
8xy7 - SUBN Vx, Vy
Set Vx = Vy - Vx, set VF = NOT borrow.
If Vy > Vx, then VF is set to 1, otherwise 0. Then Vx is subtracted from Vy, and the results stored in Vx.
| |
8xyE - SHL Vx {, Vy}
Set Vx = Vx SHL 1.
If the most-significant bit of Vx is 1, then VF is set to 1, otherwise to 0. Then Vx is multiplied by 2.
A left shift is performed (multiplication by 2), and the most significant bit is saved in Register VF.
| |
9xy0 - SNE Vx, Vy
Skip next instruction if Vx != Vy.
Since our PC has already been incremented by 2 in Cycle(), we can just increment by 2 again to skip the next instruction.
| |
Annn - LD I, addr
Set I = nnn.
| |
Bnnn - JP V0, addr
Jump to location nnn + V0.
| |
Cxkk - RND Vx, byte
Set Vx = random byte AND kk.
| |
Dxyn - DRW Vx, Vy, nibble
Display n-byte sprite starting at memory location I at (Vx, Vy), set VF = collision.
We iterate over the sprite, row by row and column by column. We know there are eight columns because a sprite is guaranteed to be eight pixels wide.
If a sprite pixel is on then there may be a collision with what’s already being displayed, so we check if our screen pixel in the same location is set. If so we must set the VF register to express collision.
Then we can just XOR the screen pixel with 0xFFFFFFFF to essentially XOR it with the sprite pixel (which we now know is on). We can’t XOR directly because the sprite pixel is either 1 or 0 while our video pixel is either 0x00000000 or 0xFFFFFFFF.
| |
Ex9E - SKP Vx
Skip next instruction if key with the value of Vx is pressed.
Since our PC has already been incremented by 2 in Cycle(), we can just increment by 2 again to skip the next instruction.
| |
ExA1 - SKNP Vx
Skip next instruction if key with the value of Vx is not pressed.
Since our PC has already been incremented by 2 in Cycle(), we can just increment by 2 again to skip the next instruction.
| |
Fx07 - LD Vx, DT
Set Vx = delay timer value.
| |
Fx0A - LD Vx, K
Wait for a key press, store the value of the key in Vx.
The easiest way to “wait” is to decrement the PC by 2 whenever a keypad value is not detected. This has the effect of running the same instruction repeatedly.
| |
Fx15 - LD DT, Vx
Set delay timer = Vx.
| |
Fx18 - LD ST, Vx
Set sound timer = Vx.
| |
Fx1E - ADD I, Vx
Set I = I + Vx.
| |
Fx29 - LD F, Vx
Set I = location of sprite for digit Vx.
We know the font characters are located at 0x50, and we know they’re five bytes each, so we can get the address of the first byte of any character by taking an offset from the start address.
| |
Fx33 - LD B, Vx
Store BCD representation of Vx in memory locations I, I+1, and I+2.
The interpreter takes the decimal value of Vx, and places the hundreds digit in memory at location in I, the tens digit at location I+1, and the ones digit at location I+2.
We can use the modulus operator to get the right-most digit of a number, and then do a division to remove that digit. A division by ten will either completely remove the digit (340 / 10 = 34), or result in a float which will be truncated (345 / 10 = 34.5 = 34).
| |
Fx55 - LD [I], Vx
Store registers V0 through Vx in memory starting at location I.
| |
Fx65 - LD Vx, [I]
Read registers V0 through Vx from memory starting at location I.
| |
Function Pointer Table
The easiest way to decode an opcode is with a switch statement, but it gets messy when you have a lot of instructions. The CHIP-8 isn’t so bad, but we’ll use a different technique that is more scalable and good to know when making more advanced emulators.
Instead we’ll implement an array of function pointers where the opcode is an index into an array of function pointers. The downside to a function pointer table is that we must have an array big enough to account for every opcode because the opcode is an index into the array. Dereferencing a pointer for every instruction may also have problems, but when your emulator is complex it’s probably worth it.
If you look at the list of opcodes, you’ll notice that there are four types:
- The entire opcode is unique:
- $1nnn
- $2nnn
- $3xkk
- $4xkk
- $5xy0
- $6xkk
- $7xkk
- $9xy0
- $Annn
- $Bnnn
- $Cxkk
- $Dxyn
- The first digit repeats but the last digit is unique:
- $8xy0
- $8xy1
- $8xy2
- $8xy3
- $8xy4
- $8xy5
- $8xy6
- $8xy7
- $8xyE
- The first three digits are $00E but the fourth digit is unique:
- $00E0
- $00EE
- The first digit repeats but the last two digits are unique:
- $ExA1
- $Ex9E
- $Fx07
- $Fx0A
- $Fx15
- $Fx18
- $Fx1E
- $Fx29
- $Fx33
- $Fx55
- $Fx65
The first digits go from $0 to $F so we’ll need an array of function pointers that can be indexed up to $F, which requires $F + 1 elements.
For the opcodes with first digits that repeat ($0, $8, $E, $F), we’ll need secondary tables that can accommodate each of those.
- $0 needs an array that can index up to $E+1
- $8 needs an array that can index up to $E+1
- $E needs an array that can index up to $E+1
- $F needs an array that can index up to $65+1
In the master table, we set up a function pointer to a function that then indexes correctly based on the relevant parts of the opcode.
Just in case one of the invalid opcodes is called, we can create a dummy OP_NULL function that does nothing, but will be the default function called if a proper function pointer is not set.
| |
Fetch, Decode, Execute
When we talk about one cycle of this primitive CPU that we’re emulating, we’re talking about it doing three things:
- Fetch the next instruction in the form of an opcode
- Decode the instruction to determine what operation needs to occur
- Execute the instruction
The decoding and executing are done with the function pointers we just implemented. We get the first digit of the opcode with a bitmask, shift it over so that it becomes a single digit from $0 to $F, and use that as index into the function pointer array. It’s then further decoded in the Table() method.
| |
The Platform Layer
We’ll use SDL to render and get input in a multi-platform way. Using an SDL_Renderer gives us 2D GPU acceleration, and an SDL_Texture is an easy way to render a 2D image. Consult the SDL documentation for more specific information.
| |
The Main Loop
Finally we need our main loop that will call our Chip8::Cycle() function continuously until exit, handle input, and render with SDL.
We’ll use three command-line arguments:
- Scale: The CHIP-8 video buffer is only 64x32, so we’ll need an integer scale factor to be able to play on our big modern monitors.
- Delay: The CHIP-8 had no specified clock speed, so we’ll use a delay to determine the time in milliseconds between cycles. Different games run best at different speeds, so we can control it here.
- ROM: The ROM file to load.
With each iteration of the loop: input from the keyboard is parsed, a delay is checked to see if enough time has passed between cycles and a cycle is run if so, and the screen is updated.
Due to the way SDL works, we can simply pass in the video parameter to SDL and it will scale it automatically for us to the size of our window texture.
| |
Results
We can use this test ROM to ensure that our CPU is operating like we expect.
| |

Let’s also test our input by playing a game: Tetris. I’ve found a delay of 3 or 4 is pretty good.
| |
Conclusion
Congratulations! We’ve successfully built a very simple emulator. Hopefully you’ve learned something about emulators, bit-twiddling, logic, CPU operations, and more. Take that knowledge and put it to use in other programming endeavors, or move onto building an NES emulator. That’s what I’ll be doing.
Appendix: Bits, Bytes, Etc.
Low-level bit manipulation is a very important part of this project, so if you need a primer or refresher, here it is.
Binary
Computers operate on numbers in the form of binary, which is base-2. Any number can be presented in binary. There is a pattern to binary that helps with understanding it. Here is the sequence from 0 to 15:
| |
If we label each bit starting from Bit 3 on the left to Bit 0 on the right, we can see a pattern. Bit 0 alternates off and on with every number. Bit 1 alternates at 1/2 the rate of Bit 1. Bit 2 alternates at 1/4 the rate of Bit 1. And Bit 3 alternates at 1/8 the rate of Bit 1.
With our base-10 system, numbers count up from 0 to 9 and then shift over to the left when we grow larger than what 9 can represent. 9 becomes 10. 19 becomes 20. 29 becomes 30. And so on.
Binary is no different, only it’s base-2, so we only have 0 and 1. We go from 0b0001 to 0b0010. 0b0011 to 0b0100. 0b0111 to 0b1000.
In base-10, we can get any digit with a sum. Remember talking about the “ones place”, the “tens place”, the “hundreds place”, etc? The base-10 number 216 has a 2 in the hundreds place, a 1 in the tens place, and a 6 in the hundreds place. 206 can then be created by multiplying each digit by its place and summing them all: \((2 \cdot 10^2) + (1 \cdot 10^1) + (6 \cdot 10^0) = 216\)
Again, binary is no different, only you have a ones place, a twos place, a fours place, etc. The binary number 0b101 has a 1 in the fours place, a 0 in the twos place, and a 1 in the ones place: \((1 \cdot 2^2) + (0 \cdot 2^1) + (1 \cdot 2^0) = 5\)
Bit 3 is called the Most Significant Bit (MSB) because it contributes the most to the final value of the number (because its the eights place). Bit 0 is called the Least Significant Bit (LSB) because it contributes the least to the final value (because it’s the ones place).
Hexadecimal
Reading binary becomes difficult for a human after about four bits though, so we often use hexadecimal (hex) which is base-16. While base-2 has 0 and 1, and base-10 has 0 through 9, base-16 has 0 through 9 and A through F. The principles of counting it are the same as base-2 and base-10, there are just now letters involved.
- A = 10
- B = 11
- C = 12
- D = 13
- E = 14
- F = 15.
The hex number 0xBEEF is \((B \cdot 16^3) + (E \cdot 16^2) + (E \cdot 16^1) + (F \cdot 16^0) = 48879\)
In binary that would be 0b1011111011101111, which is much less pleasant to the human experience.
Bits and Bytes
A single binary digit is called a bit. Because it’s binary, it can either be ON (1) or OFF (0).
Eight bits make a byte, so a byte can go as high as \(2^8 = 255\). In hex that is 0xFF.
The common multiples you will see are 1 byte (0xFF), 2 bytes (0xFFFF), 4 bytes (0xFFFFFFFF), and 8 bytes (0xFFFFFFFFFFFFFFFF).
AND, OR, NOT, XOR
Beyond understanding how to read binary and hex, you need to know how to manipulate them with some common operations: AND, OR, and XOR.
They are explained most concisely in table form:
| |
AND is true if both bits are true. OR is true if either bit is true. NOT toggles the bit. XOR is true if only a single bit is true.
In C++, AND is using the symbol &, OR uses the symbol |, NOT uses the symbol ~, and XOR uses the symbol ^.
Bitmasking
AND and OR are especially useful for bitmasking, where you can manipulate a binary number with another binary number.
AND is good for clearing bits.
Let’s say we have the binary number 0b0110 and we want to clear Bit 1. We can AND it with 0b1101. The 0 will clear the bit if it’s set (1 AND 0 = 0), but any set bits will stay set (1 AND 1 = 1).
| |
OR is good for setting bits.
Let’s say we have the binary number 0b0110 and we want to set Bit 3. We can OR it with 0b1000. The 1 will set the bit if it’s not set (1 OR 0 = 1), but any unset bits will stay unset (0 OR 1 = 0).
| |
NOT is good for toggling bits.
Let’s say we have the binary number 0b0110 and we want to toggle the off bits on and the on bits off. We can use the NOT operation.
| |
XOR is good for many things, but one common application in CPUs is to clear a register by XORing it with itself.
Let’s say we have the binary number 0b0110 and we want to clear it all to zeros without using any other numbers. We can use XOR.
| |
Bit Shifting
Bit shifting is the act of moving the bits of a number left or right. A left shift is equivalent to multiplying by 2 and a right shift is equivalent to dividing by 2.
| |
Source Code
You can find all of the code here.
Last Edited: Jun 19, 2024