Building an FPGA Computer: SAP-2

Previously I built the SAP-1 on an FPGA based on a design laid out in the book Digital Computer Electronics by Malvino and Brown. Now it’s time to build the SAP-2, also from the book, which is quite a large step up from the SAP-1.

While the SAP-1 was explained in great detail in the book, the SAP-2 is much more vague and undefined. They don’t go into implementation details, provide schematics, or show the control signals. Instead they give a brief functional overview of its components, list out its instructions, and that’s about it. Thus I was forced to figure things out on my own, for better or for worse.

When creating my FPGA version, I decided to be content with it being functionally identical without getting hung up on the implementation details. As such, a program run on their theoretical version would have the same output as on mine, but the way it got there and the time it took to do it would be different.

This post is intended as a supplement to the first so I’ll assume readers of this one are familiar already with the SAP-1 to save me from repeating myself. I’ll refer back to it and mention ways that the SAP-2 differs.

Overview

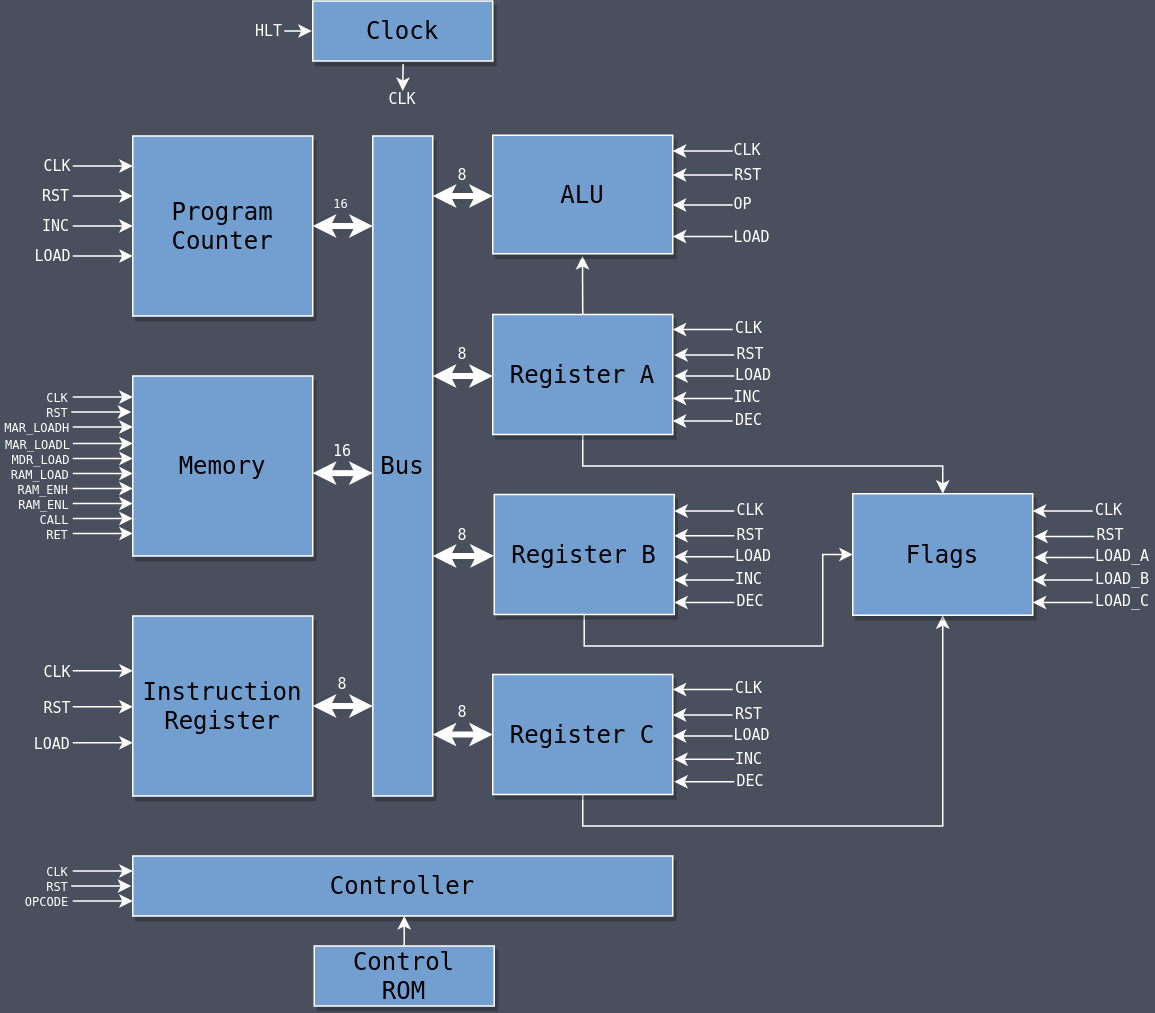
Modules

Clock

The clock is unchanged from the SAP-1.

1
2
3
4
5
6
7
8
9

module clock(
	input hlt,
	input clk_in,
	output clk_out
);

assign clk_out = (hlt) ? 1'b0 : clk_in;

endmodule

Program Counter

The program counter has been widened to 16 bits and it has an additional load signal.

The load signal loads the PC with a value taken from the bus, a requirement for being able to jump around during a program’s execution.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

module pc(
	input clk,
	input rst,
	input inc,
	input load,
	input[15:0] bus,
	output[15:0] out
);

reg[15:0] pc;

always @(posedge clk, posedge rst) begin
	if (rst) begin
		pc <= 16'b0;
	end else if (load) begin
		pc <= bus;
	end else if (inc) begin
		pc <= pc + 1;
	end
end

assign out = pc;

endmodule

Registers A/B/C

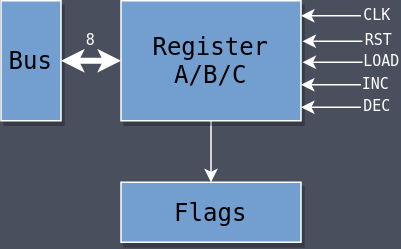
There are now three registers: A, B, and C. Each are functionally identical so there is a single register module that is used for all three. It’s instantiated three times in the top module and given different names for each.

The book briefly mentions that register increments and decrements are done using the ALU, which would require putting a 1 into the ALU’s temp register, putting the contents of B or C into A, and then doing an addition or a subtraction. But it doesn’t explain where that 1 comes from, how to avoid the A register being overwritten for increments and decrements of B or C, or how it’s supposed to be done in only four T-states.

I instead opted to give each register an inc and a dec signal to increment and decrement, respectively, rather than go through the ALU. I may figure out a way to use the ALU directly when it comes time to build the SAP-3.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

module register(
	input clk,
	input rst,
	input load,
	input inc,
	input dec,
	input[15:0] bus,
	output[7:0] out
);

reg[7:0] data;

always @(posedge clk, posedge rst) begin
	if (rst) begin
		data <= 8'b0;
	end else if (load) begin
		data <= bus[7:0];
	end else if (inc) begin
		data <= data + 1;
	end else if (dec) begin
		data <= data - 1;
	end
end

assign out = data;

endmodule

ALU

The Arithmetic Logic Unit (ALU) is the same as the SAP-1’s Adder but with the ability to do logic operations.

The temporary register has been moved inside of the ALU module itself which can be loaded with the load signal which frees up Register B for other uses. Register A continues to be the primary register for operations, using the temp register as the other operand when required. The control logic is responsible for filling the temp register with the necessary data prior to doing the operation.

The ALU can perform eight operations:

• Addition (ADD)
• Subtraction (SUB)
• Logical AND (AND)
• Logical OR (OR)
• Logical XOR (XOR)
• Complement (CMA)
• Rotate All Left (RAL)
• Rotate All Right (RAR)

An arithmetic shift left will move the bits that are shifted out the left side into the right side, while an arithmetic shift right will move zeroes into the left side.

The operation to be performed is determined by the op signal.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

module alu(
	input clk,
	input rst,
	input[7:0] a,
	input[2:0] op,
	input load,
	input[15:0] bus,
	output[7:0] out
);

reg[7:0] alu;
reg[7:0] tmp;

localparam OP_ADD = 0;
localparam OP_SUB = 1;
localparam OP_AND = 2;
localparam OP_OR  = 3;
localparam OP_XOR = 4;
localparam OP_CMA = 5;
localparam OP_RAL = 6;
localparam OP_RAR = 7;

always @(posedge clk, posedge rst) begin
	if (rst) begin
		tmp <= 8'b0;
	end else if (load) begin
		tmp <= bus[7:0];
	end
end

always @(*) begin
	case (op)
		OP_ADD: begin
			alu = a + tmp;
		end
		OP_SUB: begin
			alu = a - tmp;
		end
		OP_AND: begin
			alu = a & tmp;
		end
		OP_OR: begin
			alu = a | tmp;
		end
		OP_XOR: begin
			alu = a ^ tmp;
		end
		OP_CMA: begin
			alu = ~a;
		end
		OP_RAL: begin
			alu = a << 1;
			alu[0] = a[7];
		end
		OP_RAR: begin
			alu = a >> 1;
		end
		default: begin
			alu = 0;
		end
	endcase
end

assign out = alu;

endmodule

Flags Register

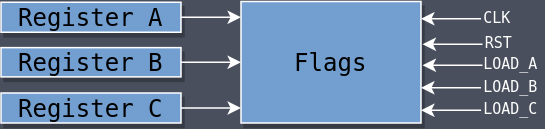
The flags register is a special register used to hold the status of previous operations. There are two:

• Zero Flag: Set if the previous operation caused a result of 0.
• Sign Flag: Set if the previous operation caused a negative result.

It’s a bit unusual that the flags register is connected to A/B/C directly instead of to the ALU, but that was required so that the INR and DCR instructions would update the flags without going through the ALU, as discussed above.

Not all instructions should update the flags so there are three signals that dictate whether or not the flags are updated based on the contents of each of the three registers: load_a, load_b, and load_c.

For example, INR C operates on Register C, so the control logic asserts load_c so that the flags are updated based on the contents of C. If the increment operation causes C to become zero then FLAG_Z is set. If the operation causes C to become negative then FLAG_S is set.

But the instruction MVI C, A, which copies the contents of A into C, should not update the flags, and so the load_c signal is not asserted during that instruction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

module flags(
	input clk,
	input rst,
	input[7:0] a,
	input[7:0] b,
	input[7:0] c,
	input load_a,
	input load_b,
	input load_c,
	output[1:0] out
);

localparam FLAG_Z = 1;
localparam FLAG_S = 0;

reg[1:0] flags;

always @(negedge clk, posedge rst) begin
	if (rst) begin
		flags <= 2'b0;
	end else if (load_a) begin
		flags[FLAG_Z] <= (a == 0) ? 1'b1 : 1'b0;
		flags[FLAG_S] <= (a[7] == 1) ? 1'b1 : 1'b0;
	end else if (load_b) begin
		flags[FLAG_Z] <= (b == 0) ? 1'b1 : 1'b0;
		flags[FLAG_S] <= (b[7] == 1) ? 1'b1 : 1'b0;
	end else if (load_c) begin
		flags[FLAG_Z] <= (c == 0) ? 1'b1 : 1'b0;
		flags[FLAG_S] <= (c[7] == 1) ? 1'b1 : 1'b0;
	end
end

assign out = flags;

endmodule

Memory

The memory has been expanded to 64K which requires a 16-bit address space to be able to address from 0x0000 to 0xFFFF. The expansion to 16-bit requires more complicated control logic which requires more control signals.

The Memory Address Register (MAR) holds memory address so it was expanded to 16-bit which required separate signals for loading the high byte (mar_loadh) and the low byte (mar_loadl).

There is also a new internal register called the Memory Data Register (MDR) which holds values temporarily when reading from or writing to the memory. mdr_load loads into the MDR from the bus and ram_load loads into memory from the MDR.

The MDR is 16-bit even though data values should only be 8-bit because certain instructions (namely LDA and STA) require holding two separate values in the MDR at one time. The high byte is loaded with ram_enh and the low byte is loaded with ram_enl. I’m not sure if this was what Malvino and Brown had in mind but it works.

The call signal loads two special memory locations (0xFFFE and 0xFFFF) with the contents of the bus and the ret signal loads from those two locations into the MDR to be later put back into the PC. These two signals are used to facilitate the CALL and RET instructions which will be discussed later. The implication of this rudimentary system is that a function cannot call another function or else the return address will be overwritten. The SAP-3 will fix that.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

module memory(
	input clk,
	input rst,
	input mar_loadh,
	input mar_loadl,
	input mdr_load,
	input ram_load,
	input ram_enh,
	input ram_enl,
	input call,
	input ret,
	input[15:0] bus,
	output[15:0] out
);

initial begin
	$readmemh("program.bin", ram);
end

reg[15:0] mar;
reg[15:0] mdr;
reg[7:0]  ram[0:65535];

always @(posedge rst) begin
	mar <= 16'b0;
	mdr <= 16'b0;
end

always @(posedge clk) begin
	if (mar_loadh) begin
		mar[15:8] <= bus[15:8];
	end

	if (mar_loadl) begin
		mar[7:0] <= bus[7:0];
	end

	if (mdr_load) begin
		mdr[7:0] <= bus[7:0];
	end

	if (ret) begin
		mdr[15:8] <= ram[16'hFFFE];
		mdr[7:0] <= ram[16'hFFFF];
	end else if (call) begin
		ram[16'hFFFE] <= bus[15:8];
		ram[16'hFFFF] <= bus[7:0];
	end else if (ram_enh) begin
		mdr[15:8] <= ram[mar];
	end else if (ram_enl) begin
		mdr[7:0] <= ram[mar];
	end else if (ram_load) begin
		ram[mar] <= mdr;
	end
end

assign out = mdr;

endmodule

Instruction Register

The Instruction Register (IR) is unchanged from the SAP-1 except that it only uses the lower eight bits of the bus during a load.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

module ir(
	input clk,
	input rst,
	input load,
	input[15:0] bus,
	output[7:0] out
);

reg[7:0] ir;

always @(posedge clk, posedge rst) begin
	if (rst) begin
		ir <= 8'b0;
	end else if (load) begin
		ir <= bus[7:0];
	end
end

assign out = ir;

endmodule

Instructions

There are 39 instructions which is a lot more than the SAP-1. The book also includes an IN and an OUT but I removed those because they don’t make sense for the version I’m building.

The book uses the same opcodes for the instructions as the Intel 8080 and I did the same to stay consistent. The authors provide the number of T-states that are required for each instruction but I was unable to reach the same values for many of the instructions. In some cases my implementation uses fewer T-states and in some others it uses more.

In particular, the INR and DCR instructions don’t make sense as described by Malvino and Brown. They claim that those two instructions use Register A for those operations but if that were true then the contents of A would be lost and it would take a lot more than four T-states as they claim. I decided to use explicit inc and dec signals for each of the three main registers to allow for directly incrementing and decrementing them in a single T-state.

Some instructions update the flags and some do not. If an instruction operates on a particular register then the flags are updated based on the conditions of that register (e.g., INR B will update the flags if B becomes 0 or negative).

There are four Address Modes:

• Direct
  • Required data is located at memory address which follows the opcode
• Immediate
  • Required data is specified in the instruction itself
• Register
  • Required data is inside of a register
• Implied
  • Required data is implied by the opcode

Every instruction takes at least three T-states because it takes three just to fetch the instruction from memory. The instructions with the most T-states are those that deal deal with memory addresses because of the time required to shuffle addresses from the PC to the MAR and MDR.

JM, JNZ, and JZ take a variable number of cycles depending on whether the jump occurs or not. If the jump occurs it takes eight T-states, otherwise it takes four.

The length of my instructions differ from those in the book and are faster in many places, but not all. I tried to think of solutions that would match theirs exactly but was unable to figure out how they get their numbers.

Bus

The bus has been widened to 16 bits to accommodate the memory address space and, like the SAP-1, a multiplexor is used to select which module gets to output onto the bus at any one time.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

reg[15:0] bus;

always @(*) begin
	if (a_en) begin
		bus = a_out;
	end else if (b_en) begin
		bus = b_out;
	end else if (c_en) begin
		bus = c_out;
	end else if (alu_en) begin
		bus = alu_out;
	end else if (pc_en) begin
		bus = pc_out;
	end else if (mdr_en) begin
		bus = mem_out;
	end else begin
		bus = 16'b0;
	end
end

Controller

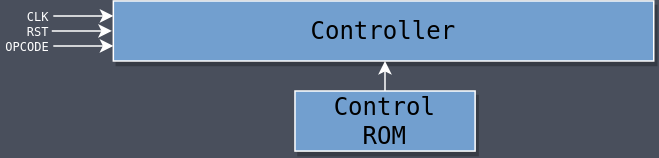
The SAP-2 has 35 control signals (23 more than the SAP-1) and the longest instruction takes 10 T-states (four more than the longest SAP-1 instruction). Trying to implement all of that logic with a switch statement like we did for the SAP-1 would result in a massive module that would be hard to write, hard to understand, and hard to debug.

Fortunately control logic is combinational logic, and all combinational logic can be represented in the form of Read-Only Memory (ROM) by using the inputs to the combinational logic to address into the ROM. The value stored at that address is the output corresponding to those inputs.

Every instruction is one byte (eight bits) and the maximum required number of T-states is 10 (requiring four bits to represent). We can combine those together into a single 12-bit address. The instruction goes into bits 11-4 and the T-state value goes into bits 3-0: IIIIIIII TTTT. Then, if we want to know what control signal should be asserted for a given instruction and certain T-state, we can look it up in the ROM.

For example, if the instruction is ADD B ($80) and we’re on stage 3, we concatenate $80 and $3 together to get address $803. The value at that address is the 35-bit control word detailing which signals to assert at that point in time. In this case: 00000001000000000000100000000000000, where the two asserted signals are B_EN and ALU_LOAD.

The question is: how to fill out the ROM? A 12-bit address means 4096 different values to program which would be a major pain (and error-prone) to do by hand. Instead I used a spreadsheet where the rows are the addresses and the columns are the different control signals and used the CONCATENATE() function to concatenate all of the signal bits into a single string. Then it was just a matter of copying that entire binary string column into a file which could be loaded in Verilog using readmemb.

A lot of space is wasted because because the 12-bit address allows for 256 instructions but there are only 41. If the SAP-2 wasn’t using a subset of the Intel 8080 instruction set then the instruction op codes could start at $00 and go up to $25, reducing the number of address lines required to six. But using the 8080 instruction set means we can use existing 8080 programs which is useful.

Given that the control ROM contains all of the logic, the actual controller itself doesn’t do much anymore. Mostly it just handles the special logic required for the jump instructions, where it checks the flag states if the current instruction is JZ, JNZ, or JM, and if it’s currently in stage 4, which is where a decision needs to be made.

Other than that, it increments the stage like usual, and pulls the current control word out of the ROM based on the current instruction and stage acting as the address.

There is also a special signal called END which is used to reset the stage back to 0 when an instruction has finished so that all 16 possible T-states don’t have to cycle through before the next instruction begins. Every instruction ends with that signal asserted, as shown in the spreadsheet image above.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

module controller(
	input clk,
	input rst,
	input[7:0] opcode,
	input[1:0] flags,
	output[33:0] out
);

localparam SIG_END       = 34;
localparam SIG_HLT       = 33;
localparam SIG_A_LOAD    = 32;
localparam SIG_A_EN      = 31;
localparam SIG_A_INC     = 30;
localparam SIG_A_DEC     = 29;
localparam SIG_B_LOAD    = 28;
localparam SIG_B_EN      = 27;
localparam SIG_B_INC     = 26;
localparam SIG_B_DEC     = 25;
localparam SIG_C_LOAD    = 24;
localparam SIG_C_EN      = 23;
localparam SIG_C_INC     = 22;
localparam SIG_C_DEC     = 21;
localparam SIG_FLAGS_LDA = 20;
localparam SIG_FLAGS_LDB = 19;
localparam SIG_FLAGS_LDC = 18;
localparam SIG_ALU_OP2   = 17;
localparam SIG_ALU_OP1   = 16;
localparam SIG_ALU_OP0   = 15;
localparam SIG_ALU_LD    = 14;
localparam SIG_ALU_EN    = 13;
localparam SIG_IR_LOAD   = 12;
localparam SIG_PC_INC    = 11;
localparam SIG_PC_LOAD   = 10;
localparam SIG_PC_EN     = 9;
localparam SIG_MAR_LOADH = 8;
localparam SIG_MAR_LOADL = 7;
localparam SIG_MDR_LOAD  = 6;
localparam SIG_MDR_EN    = 5;
localparam SIG_RAM_LOAD  = 4;
localparam SIG_RAM_ENH   = 3;
localparam SIG_RAM_ENL   = 2;
localparam SIG_CALL      = 1;
localparam SIG_RET       = 0;

localparam OP_JZ  = 8'hCA;
localparam OP_JNZ = 8'hC2;
localparam OP_JM  = 8'hFA;

localparam FLAG_Z = 1;
localparam FLAG_S = 0;

reg[34:0] ctrl_word;

reg[34:0] ctrl_rom[0:4095];
initial begin
	$readmemb("ctrl_rom.bin", ctrl_rom);
end

reg[3:0] stage;
always @(negedge clk, posedge rst) begin
	if (rst) begin
		stage <= 0;
	end else begin
		if (stage_rst) begin
			stage <= 0;
		end else begin
			stage <= stage + 1;
		end
	end
end

reg stage_rst;
always @(*) begin
	ctrl_word = ctrl_rom[{opcode, stage}];

	if ((opcode == OP_JZ  && stage == 4 && flags[FLAG_Z] == 0) ||
		(opcode == OP_JNZ && stage == 4 && flags[FLAG_Z] == 1) ||
		(opcode == OP_JM  && stage == 4 && flags[FLAG_S] == 0))
	begin
		stage_rst = 1;
	end else begin
		stage_rst = ctrl_rom[{opcode, stage}][SIG_END];
	end
end

assign out = ctrl_word;

endmodule

Programming

The SAP-2 uses a subset of the Intel 8080 instruction set which has the nice benefit of being able to use existing 8080 tools for our version, like an assembler. The Pretty 8080 Assembler lets you write 8080 assembly and then assembles it into various forms for you.

Here’s a perfectly valid 8080 program written in assembly using only the subset of instructions listed above:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

MVI A, 0   ; A = 0
MVI B, 12  ; B = 12
MVI C, 8   ; C = 8

REPEAT:
ADD B       ; A += B
DCR C       ; C--
JZ DONE     ; if (C == 0) go to DONE
JMP REPEAT  ; else go to REPEAT 

DONE:
HLT

Here it is annotated with addresses, opcodes, and operands:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

$0000 |  3E 00     | MVI A, 0    ; A = 0
$0002 |  06 0C     | MVI B, 12   ; B = 12
$0004 |  0E 08     | MVI C, 8    ; C = 8
      |            |
      |            | REPEAT:
$0006 |  80        | ADD B       ; A += B
$0007 |  0D        | DCR C       ; C--
$0008 |  CA 0E 00  | JZ DONE     ; if (C == 0) go to DONE
$000B |  C3 06 00  | JMP REPEAT  ; else go to REPEAT 
      |            |
      |            | DONE:
$000E |  76        | HLT

Using the HEX button in the assembler will write out the program as hex values to a file on disk, but unfortunately it also includes extra characters we don’t want. Instead we can use the BIN button to write out actual binary data instead. Then we can use a tool called hexdump to convert that to hex for us which we can then read into memory inside of Verilog.

1

hexdump -ve '8/1 "%02x " "\n"' program.com > program.bin

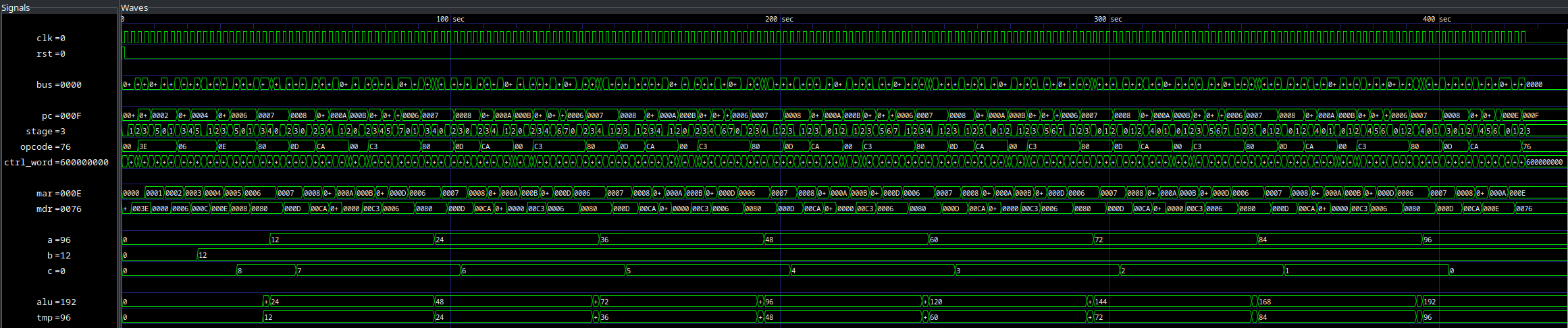
Simulation

Again we use a testbench to simulate the design and verify correctness.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191

module top_tb();


initial begin
	$dumpfile("top_tb.vcd");
	$dumpvars(0, top_tb);
	rst = 1;
	#1 rst = 0;
end

reg[15:0] bus;

always @(*) begin
	if (a_en) begin
		bus = a_out;
	end else if (b_en) begin
		bus = b_out;
	end else if (c_en) begin
		bus = c_out;
	end else if (alu_en) begin
		bus = alu_out;
	end else if (pc_en) begin
		bus = pc_out;
	end else if (mdr_en) begin
		bus = mem_out;
	end else begin
		bus = 16'b0;
	end
end

reg clk_in = 0;
integer i;
initial begin
	for (i = 0; i < 512; i++) begin
		#1 clk_in = ~clk_in;
	end
end

reg rst;
wire hlt;
wire clk;
clock clock(
	.hlt(hlt),
	.clk_in(clk_in),
	.clk_out(clk)
);

wire pc_inc;
wire pc_load;
wire pc_en;
wire[15:0] pc_out;
pc pc(
	.clk(clk),
	.rst(rst),
	.inc(pc_inc),
	.load(pc_load),
	.bus(bus),
	.out(pc_out)
);

wire ir_load;
wire[7:0] ir_out;
ir ir(
	.clk(clk),
	.rst(rst),
	.load(ir_load),
	.bus(bus),
	.out(ir_out)
);

wire mar_loadh;
wire mar_loadl;
wire mdr_load;
wire mdr_en;
wire ram_load;
wire ram_enh;
wire ram_enl;
wire call;
wire ret;
wire[15:0] mem_out;
memory mem(
	.clk(clk),
	.rst(rst),
	.mar_loadh(mar_loadh),
	.mar_loadl(mar_loadl),
	.mdr_load(mdr_load),
	.ram_load(ram_load),
	.ram_enh(ram_enh),
	.ram_enl(ram_enl),
	.call(call),
	.ret(ret),
	.bus(bus),
	.out(mem_out)
);

wire a_load;
wire a_en;
wire a_inc;
wire a_dec;
wire[7:0] a_out;
register reg_a(
	.clk(clk),
	.rst(rst),
	.load(a_load),
	.inc(a_inc),
	.dec(a_dec),
	.bus(bus),
	.out(a_out)
);

wire b_load;
wire b_en;
wire b_inc;
wire b_dec;
wire[7:0] b_out;
register reg_b(
	.clk(clk),
	.rst(rst),
	.load(b_load),
	.inc(b_inc),
	.dec(b_dec),
	.bus(bus),
	.out(b_out)
);

wire c_load;
wire c_en;
wire c_inc;
wire c_dec;
wire[7:0] c_out;
register reg_c(
	.clk(clk),
	.rst(rst),
	.load(c_load),
	.inc(c_inc),
	.dec(c_dec),
	.bus(bus),
	.out(c_out)
);

wire[2:0] alu_op;
wire alu_load;
wire alu_en;
wire[7:0] alu_out;
alu alu(
	.clk(clk),
	.rst(rst),
	.a(a_out),
	.load(alu_load),
	.op(alu_op),
	.bus(bus),
	.out(alu_out)
);

wire[1:0] flags_out;
wire flags_lda;
wire flags_ldb;
wire flags_ldc;
flags flags(
	.clk(clk),
	.rst(rst),
	.a(a_out),
	.b(b_out),
	.c(c_out),
	.load_a(flags_lda),
	.load_b(flags_ldb),
	.load_c(flags_ldc),
	.out(flags_out)
);

controller controller(
	.clk(clk),
	.rst(rst),
	.opcode(ir_out),
	.flags(flags_out),
	.out({
		hlt,
		a_load, a_en, a_inc, a_dec,
		b_load, b_en, b_inc, b_dec,
		c_load, c_en, c_inc, c_dec,
		flags_lda, flags_ldb, flags_ldc,
		alu_op, alu_load, alu_en,
		ir_load,
		pc_inc, pc_load, pc_en,
		mar_loadh, mar_loadl, mdr_load,
		mdr_en,
		ram_load, ram_enh, ram_enl,
		call, ret})
);

endmodule

Simulation generates the following waveforms, where the final value of A is 96 as expected:

Source Code

You can find all of the code here.